Carlos Bageta
Esta dirección de correo electrónico está protegida contra spambots. Necesita activar JavaScript para visualizarla.
Marcelo Alberto
Esta dirección de correo electrónico está protegida contra spambots. Necesita activar JavaScript para visualizarla.
Adrián Cecconato
Alicia Bevaqua
Marcela Garriga
Marta Tirador
Verónica Nodaro
Cátedra de Matemática. Facultad de Ciencias Agrarias, UNCUYO

La Bioeconomía definida como la ciencia de la gestión de la sustentabilidad, pretende, además de modelar matemáticamente fenómenos biológicos, como lo hace la Biomatemática, estudiar desarrollos socio-económicos sostenibles, a través de un uso eficiente de los recursos naturales.

La Matemática ofrece un amplio conjunto de procedimientos de análisis, modelación, cálculo, medición y estimación del mundo natural y social, que posibilita establecer relaciones entre los más diversos aspectos de la realidad, no sólo cuantitativas y espaciales, sino también cualitativas y predictivas. Por ello el aprendizaje de esta ciencia enriquece la comprensión de la realidad, facilita la selección de estrategias para resolver situaciones problemáticas y contribuye al desarrollo del pensamiento crítico y autónomo.

De este modo, la Matemática se constituye en una valiosa herramienta para representar fenómenos reales mediante modelaciones, porque posibilita describir, explicar y predecir. Describir, en el sentido de que los modelos matemáticos permiten sintetizar la información disponible de un proceso de la realidad sin poner mayor atención en explicar los mecanismos subyacentes; explicar, por cuanto hacen válidos supuestos sobre el fenómeno estudiado, derivando implicancias lógicas asociadas a estos supuestos; y finalmente predecir, porque permiten obtener una respuesta teórica a cambios en los factores (parámetros y variables) que no han sido observados.

Así lo entendieron, entre tantos otros matemáticos a lo largo de la historia, Alfred Lotka (Estados Unidos) y Vitto Volterra (Italia) quienes, alrededor del año 1927, valiéndose de la Matemática como herramienta de modelación, comenzaron a construir prototipos para describir procesos biológicos. Estos estudios dieron origen a una interesante ciencia interdisciplinaria, a la cual años después se la llamaría Biomatemática.

Por su parte, la Bioeconomía, definida como la ciencia de la gestión de la sustentabilidad, pretende -además de modelar matemáticamente fenómenos biológicos, como lo hace la Biomatemática- estudiar desarrollos socio-económicos sostenibles, a través de un uso eficiente de los recursos naturales.
Entendida de este modo, la Bioeconomía no se constituye como una rama de la Economía, sino como un campo de estudio que compromete diversas disciplinas, tales como la Biología, la Física, la Matemática, la Economía, entre otras.
Resulta importante destacar que esta incipiente ciencia se construye sobre el hecho establecido de que un recurso biológico no puede ser explotado en profundidad sin perder productividad. Entendiendo que toda población tiene ritmos de reproducción y muerte propios a la especie y al hábitat en el cual crece y se desarrolla, una tasa de extracción (remoción de individuos por unidad de tiempo) mayor a la tasa reproductiva, produce decaimiento en el número de individuos y normalmente, como consecuencia de ello, también disminución en la tasa reproductiva.

Por su parte, cuando una determinada población tiene una reproducción sobrante (más de lo que necesita para mantener dicho tamaño), entonces puede ser cosechada a perpetuidad sin alterar el stock.
De acuerdo con estos casos, y conforme al principio fundamental de la Bioeconomía, es posible establecer que, identificando con precisión la porción que se puede capturar de una población en crecimiento, se garantizará la estabilidad del tamaño de dicha población a lo largo del tiempo.
En consecuencia, para la generación de modelos de Bioeconomía es preciso estudiar las realidades por lo menos desde tres disciplinas:

• Desde el punto de vista biológico interesa conocer las razones que dan cuenta de la dinámica de la abundancia y distribución de recursos.
• Desde la óptica de la Economía, se deben optimizar las utilidades de las empresas extractivas, sin descuidar la preservación del recurso.
• La Matemática permite la abstracción de los elementos de dicha realidad y posibilita realizar análisis de las relaciones existentes entre las variables involucradas que se consideren relevantes.

De la gran variedad de modelos propuestos en el área bioeconómica durante la segunda mitad del siglo pasado, se presenta a continuación el fruto de uno de los trabajos que resultó ser pionero en esta área multidisciplinaria, y que estuvo inicialmente orientado a describir las consecuencias de la explotación de ciertos recursos pesqueros. Se trata del modelo bioeconómico de Gordon-Schaefer (1954) cuya forma original está dada por:

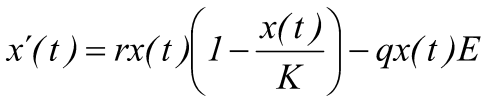
Donde:
● x(t): representa el tamaño poblacional de la especie, medido en densidad, biomasa o cantidad de individuos para un tiempo t
● x’(t): representa la tasa instantánea de crecimiento del tamaño poblacional, x(t)
● r: es la tasa intrínseca de crecimiento poblacional (que resulta ser un balance entre natalidad, mortalidad y migración propios de la especie)
● K: es la capacidad de carga del hábitat para esa especie (máximo número de individuos de la especie que el ambiente puede soportar indefinidamente, teniendo en cuenta la escasez de recursos, espacio, etc.)
● q: es el coeficiente de capturabilidad, entendido como la porción de la población que es extraída por unidad de esfuerzo
● E: es una variable que mide el nivel de esfuerzo realizado en la extracción (coeficiente asociado a la cantidad de barcos empleados, cantidad de redes, pescadores, cosechadores, entre otros).

De acuerdo con estas descripciones, la ecuación expuesta precedentemente intenta modelar el cambio instantáneo del tamaño poblacional a lo largo del tiempo en función del número de individuos de dicha población, tomando como parámetros la tasa de crecimiento natural, la capacidad de carga del sistema y la disminución de individuos de la especie producida por la actividad de cosecha.

En algunas áreas de explotación biológica, cobran mayor importancia ciertos modelos bioeconómicos denominados Modelos Impulsivos, que son útiles para representar una situación en la cual el tamaño de una población a lo largo del tiempo mantiene cierta regularidad de crecimiento, y en ciertos instantes sufre cambios abruptos por la extracción (impulsos).
El crecimiento poblacional de distintas especies puede estar expuesto a estos impactos.
Así, una población de peces cuya evolución en el tiempo pudiese modelarse asumiendo crecimiento exponencial, puede estar sometida a dos fenómenos: la pesca artesanal (aquella que llevan a cabo de forma particular los pescadores) y la pesca industrial (desarrollada por empresas con recursos y medios para efectuar altos niveles de captura en tiempos reducidos). Luego, con el propósito de conservar la evolución de estas poblaciones, los organismos de control correspondientes regulan la actividad pesquera dando libertad absoluta a los pescadores artesanales e imponiendo períodos de veda para la pesca industrial. Estas acciones determinan que el crecimiento (o el decrecimiento) de la población siga un ritmo relativamente “regular”, con irrupciones abruptas a instancias del levantamiento de vedas.

Con la finalidad de lograr un estudio más acabado del tema, se realizó un encuentro internacional denominado “Elementos de Bioeconomía Matemática” en la sede de la Facultad de Ciencias Agrarias de la UNCUYO, en el marco del proyecto de investigación “Dinámica de transiciones en interacciones poblacionales”, aprobado por la Secretaría de Ciencia, Técnica y Posgrado (SECTyP). En dichas jornadas se contó con la presencia del destacado profesor del Departamento de Matemática de la Universidad Católica del Maule, República de Chile: el Dr. Fernando Córdova Lepe.
Como fruto de estas jornadas de trabajo quedó planteada la pertinencia de modelar matemáticamente la variación poblacional respecto del paso del tiempo, en este tipo de procesos impulsivos, mediante una función definida por tramos. Dicha función debe reflejar tanto la variación “regular” ocurrida durante determinados intervalos de tiempo, tanto como las irrupciones abruptas observadas en los instantes en los que procede la intervención de la captura industrial.
En este aspecto, las ecuaciones diferenciales impulsivas son una interesante alternativa para representar matemáticamente los fenómenos descritos. De esta manera, algún sistema de ecuaciones como el que se presenta a continuación, puede representar estas variaciones poblacionales:

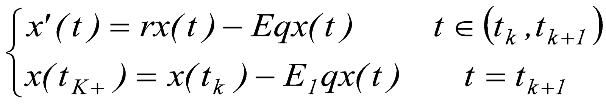
En la expresión precedente pueden observarse dos igualdades. La primera es una ecuación diferencial, que modela el comportamiento del tamaño poblacional durante intervalos de tiempo que coinciden con los periodos de veda. En ella puede verse que la razón instantánea de cambio del tamaño poblacional con respecto al tiempo, x’(t), se obtiene por la diferencia entre el crecimiento del número de individuos regido por la tasa intrínseca, y el término que refleja la captura llevada a cabo por los pescadores artesanales.
La segunda igualdad que aparece no refiere a un periodo de tiempo, sino a los instantes inmediatos posteriores (simbolizados con k+) al levantamiento de la veda para la pesca industrial. En ella no se expresa una tasa de cambio, sino la cantidad de individuos que resulta después de la captura en grandes dimensiones llevada a cabo por la pesca industrial. Esta cantidad proviene de la diferencia entre el número de individuos que conformaban la población un instante antes del levantamiento de la veda, y la cantidad de individuos extraída por la industria en el momento de levantamiento de veda. Nótese que se ha agregado un subíndice al coeficiente que muestra el esfuerzo de pesca de esta ecuación (E1) por cuanto es diferente al presentado inicialmente, en la medida de la intervención de la pesca industrial.
La siguiente gráfica de una función posibilita la visualización de este comportamiento “regular” de la variación poblacional y los oportunos “saltos” generados por pescas en grandes volúmenes.

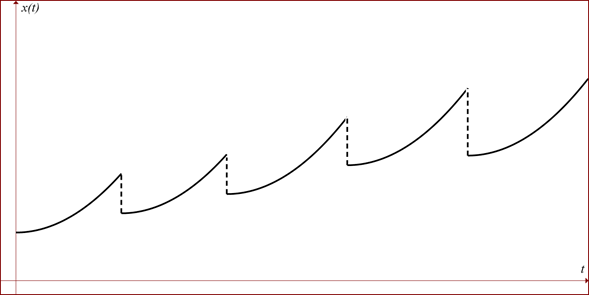
Fuente: Fernando Córdova Lepe, Dpto. de Matemática de la Universidad Católica del Maule, República de Chile.

Los modelos presentados son teóricos. Sin embargo, como se construyen siguiendo la lógica de un problema particular, pueden ser utilizados para hacer simulaciones que permitan evaluar cualitativamente propuestas de utilización de un recurso natural renovable. Además, con una adecuada calibración y validación basada en datos empíricos, estos modelos pueden ser utilizados para realizar predicciones.

Se concluye que la Bioeconomía Matemática constituye un importante aporte en los diseños de políticas de utilización de recursos.